
Chen Chen
About Me
I am a senior data visual research scientist at Dolby Laboratories. I obtained my PhD degree from University of Maryland, College Park. My research lies at the intersection of visualization, data science, and artificial intelligence. I develop mixed-initiative systems powered by AI models to support data pipelines.
News
- [July 2025] Our SVG corpus, VisAnatomy, has been accepted to IEEE VIS 2025! We demonstrate how a diverse collection of SVG charts enhances the evaluation of modern LLMs, reveals opportunities for graph learning on charts, validates prior work on chart retargeting, and supports the development of chart accessibility.
- [Feb. 2025] I have joined Dolby Laboratories as a senior data visual research scientist!
- [Nov. 2024] I have successfully defended my Ph.D. dissertation on my 30th birthday!
- [Sep. 2024] Our interactive narrative article on empirical neural network robustness has been accepted to 7th Workshop on Visualization for AI Explainability at IEEE VIS 2024!
- [July 2024] One paper presenting the computational representation of data visualization scenes, Manipulable Semantic Components, has been accepted to IEEE VIS 2024 and selected for the Honorable Mention Award (top 5%)!
- [May 2024] I have successfully advanced to candidacy, on the same day as my wedding anniversary!
- [March 2024] Our workshop paper on CLIP’s ability of analyzing fake images has been accepted to Generative AI and HCI at CHI’24! A full-paper version presenting the VA system can be seen here.
- [July 2023] Our paper on deconstructing and reusing SVG chart layouts has been accepted to IEEE VIS 2023!
- [June 2023] Our short paper on interactive notebooks for low-code visual exploratory data analysis has been accepted to VL/HCC 2023!
- [May 2023] Our State-of-the-Art (STAR) analysis on visualization corpora for automated chart analysis has been accepted to EuroVis 2023!
- [July 2021] Mascot.js (previously named Atlas), our graphics-centric visualizaiton grammar, has been accepted to IEEE VIS 2021!
Experiences

Dolby Laboratories
Senior Research Scientist
Feb. 2025 - Present

Epsilon Data Management LLC
Visualization Researcher Intern
Summer 2023

Adobe Research
Research Scientist Intern
Summer 2022
Selected Publications
-
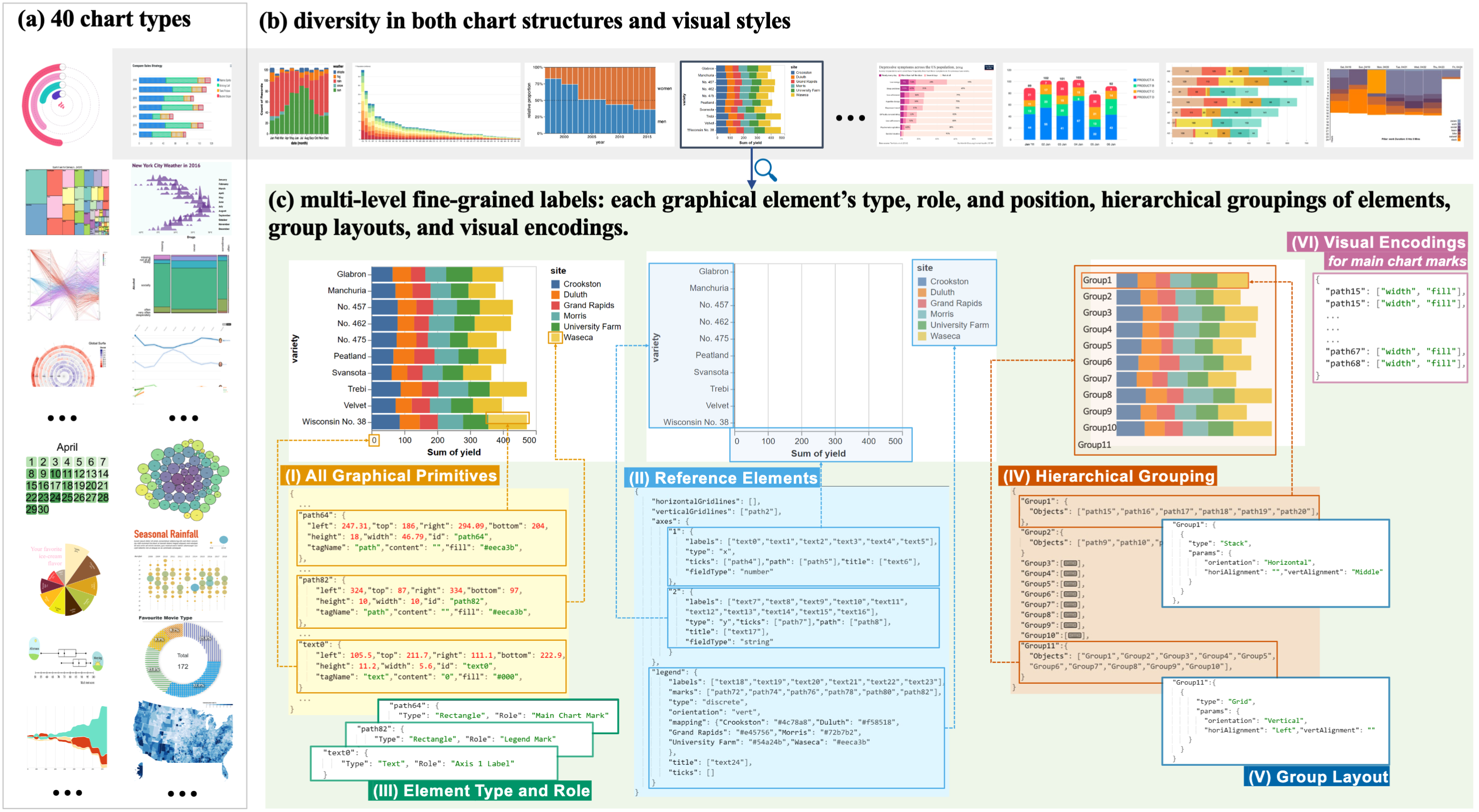 IEEE VIS 2025
IEEE Transactions on Visualization & Computer Graphics (Proceedings IEEE VIS'25), 2026
IEEE VIS 2025
IEEE Transactions on Visualization & Computer Graphics (Proceedings IEEE VIS'25), 2026 -
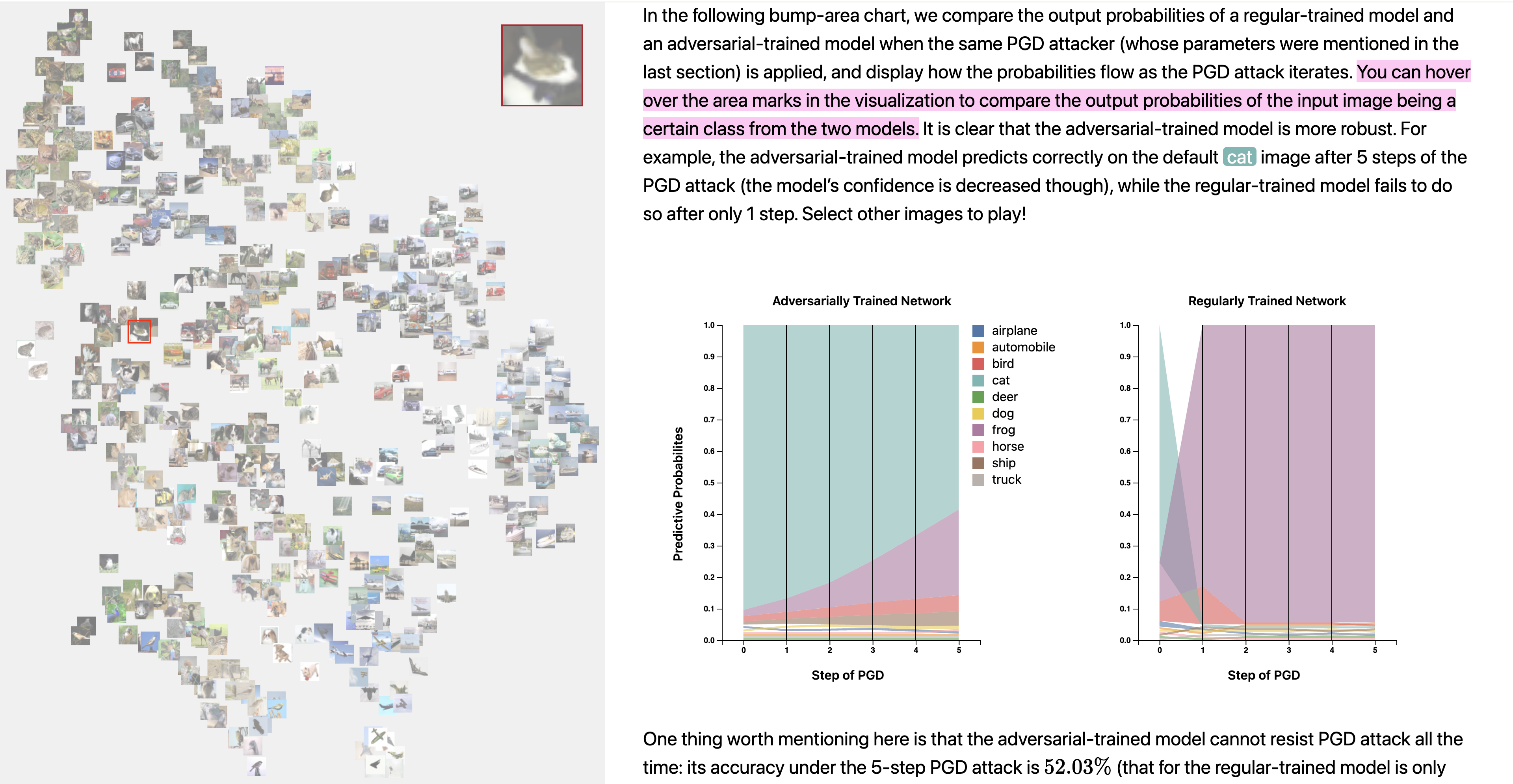 VISxAI'24
7th Workshop on Visualization for AI Explainability at IEEE VIS 2024
VISxAI'24
7th Workshop on Visualization for AI Explainability at IEEE VIS 2024 -
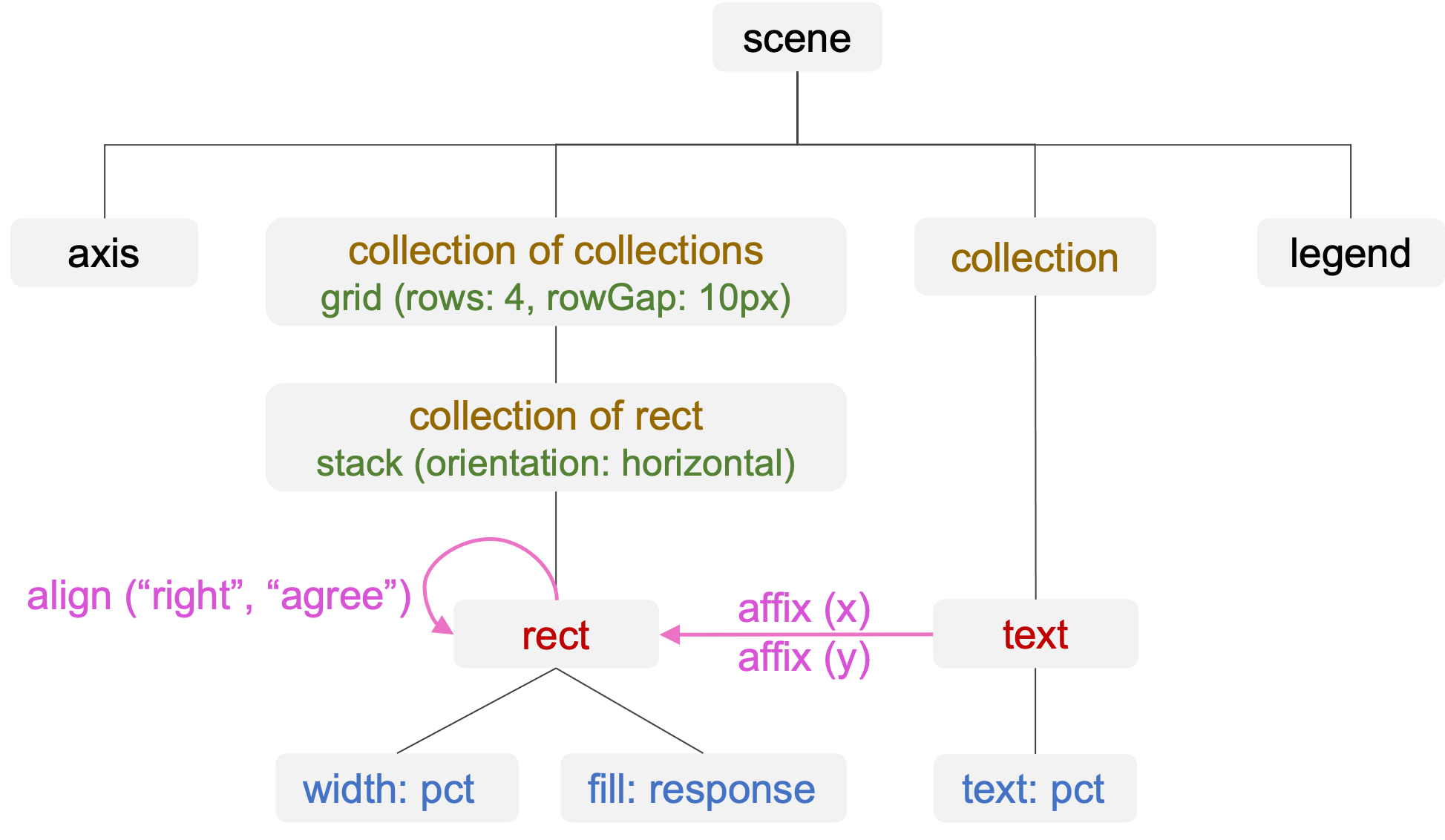 IEEE VIS 2024
IEEE Transactions on Visualization & Computer Graphics (Proceedings IEEE VIS'24), 2025
IEEE VIS 2024
IEEE Transactions on Visualization & Computer Graphics (Proceedings IEEE VIS'24), 2025 -
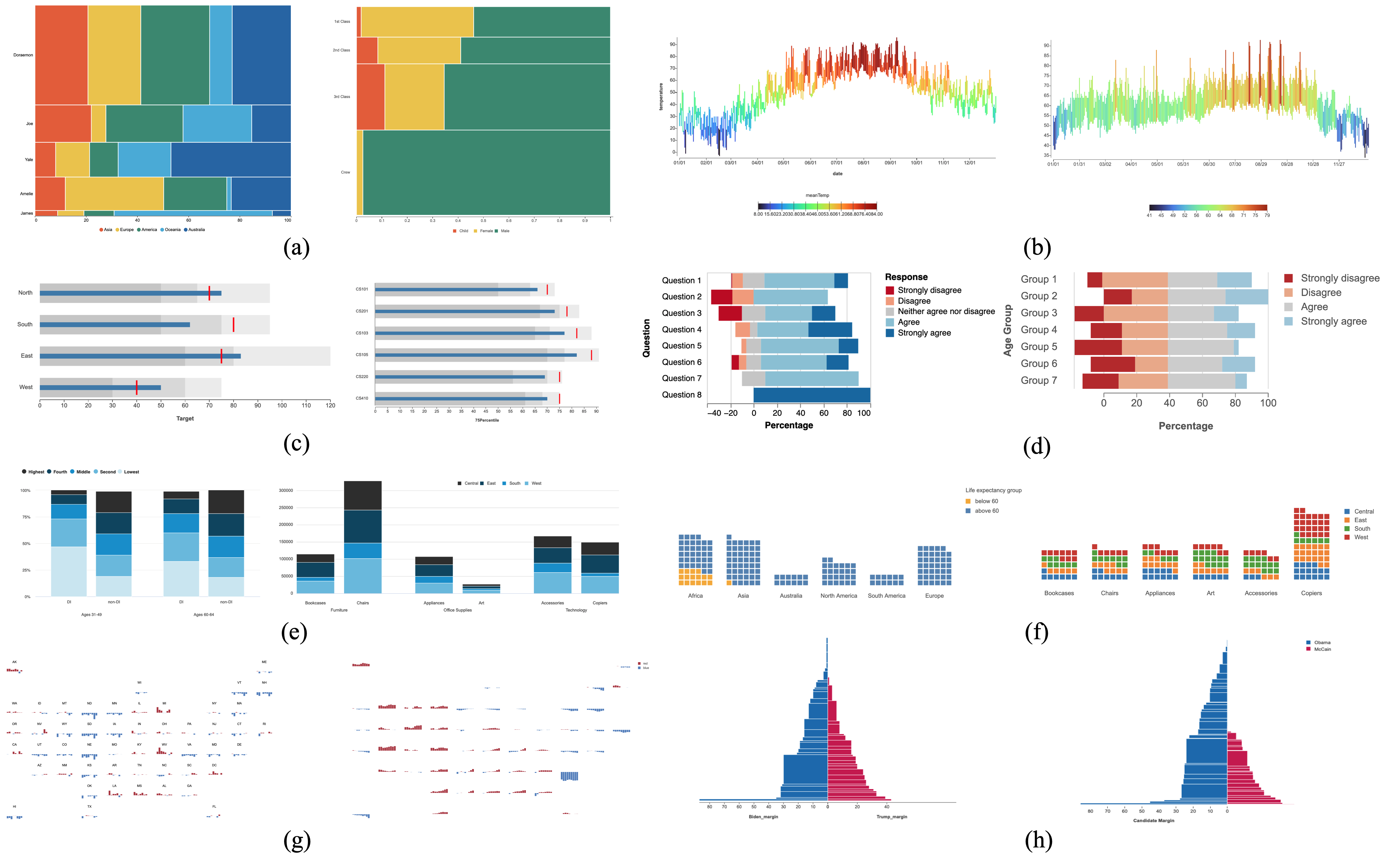 IEEE VIS 2023
IEEE Transactions on Visualization & Computer Graphics (Proceedings IEEE VIS'23), 2024
IEEE VIS 2023
IEEE Transactions on Visualization & Computer Graphics (Proceedings IEEE VIS'23), 2024 -
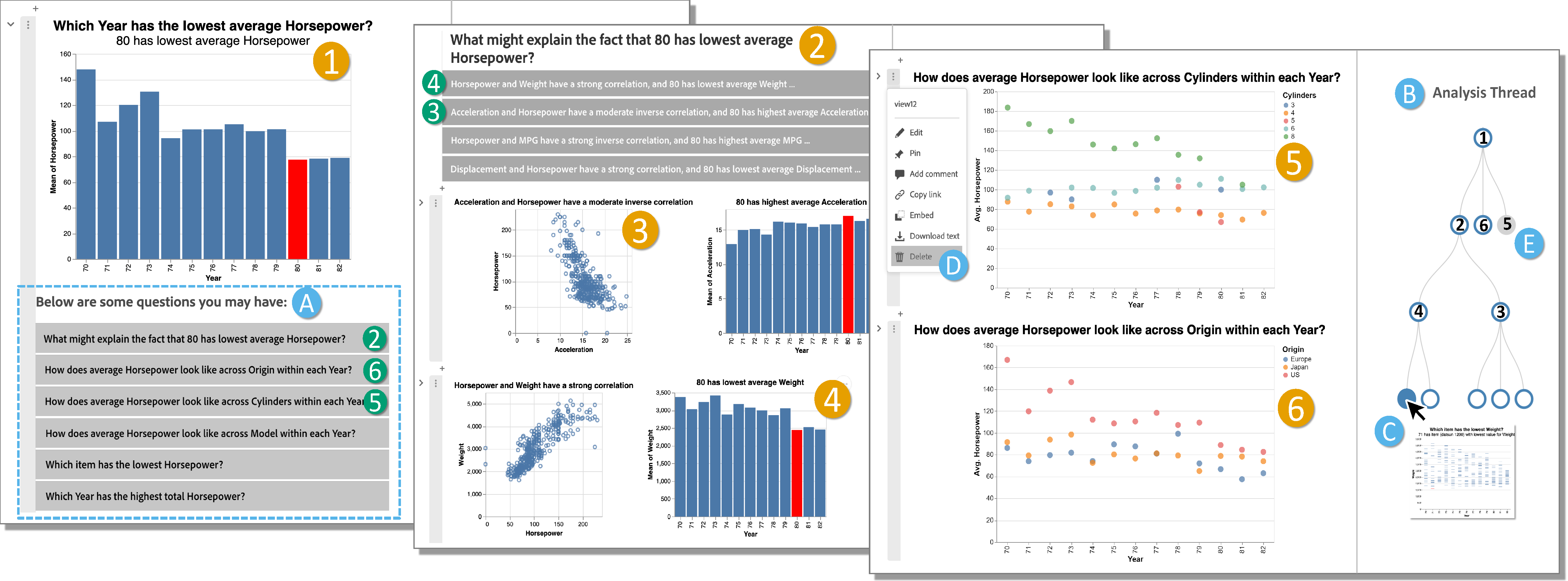 VL/HCC 2023
IEEE Symposium on Visual Languages and Human-Centric Computing (VL/HCC), 2023
VL/HCC 2023
IEEE Symposium on Visual Languages and Human-Centric Computing (VL/HCC), 2023 -
 EuroVis 2023
Computer Graphics Forum (Proceedings of EuroVis'23), 42(3), 2023
EuroVis 2023
Computer Graphics Forum (Proceedings of EuroVis'23), 42(3), 2023 -
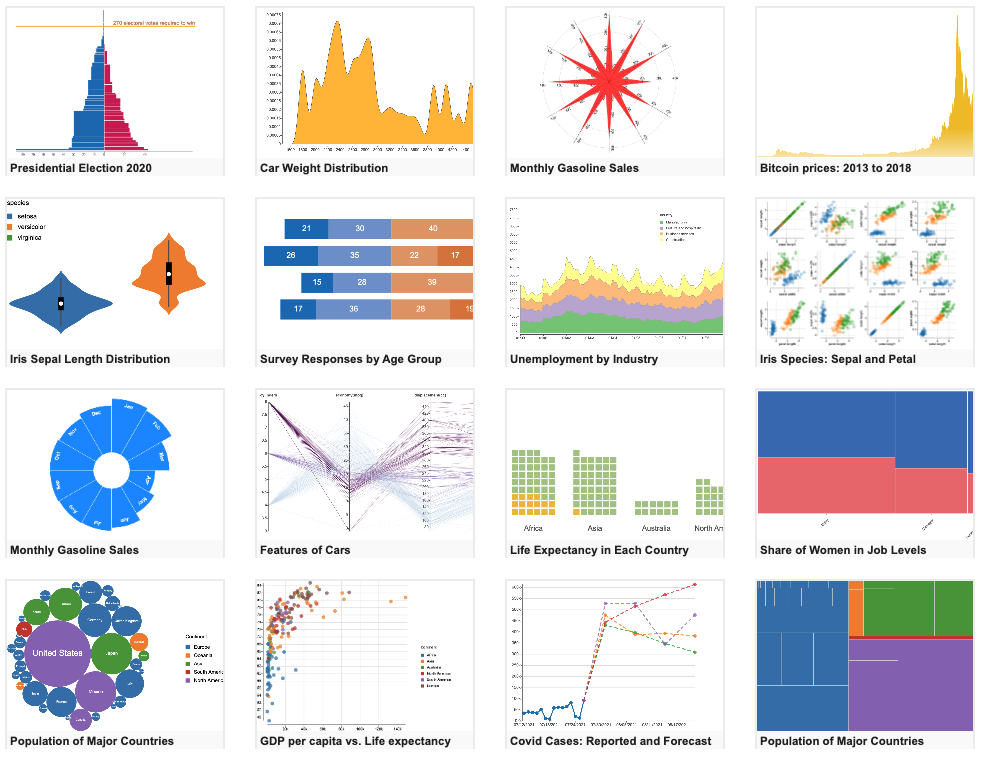 IEEE VIS 2021
IEEE VIS 2021
-
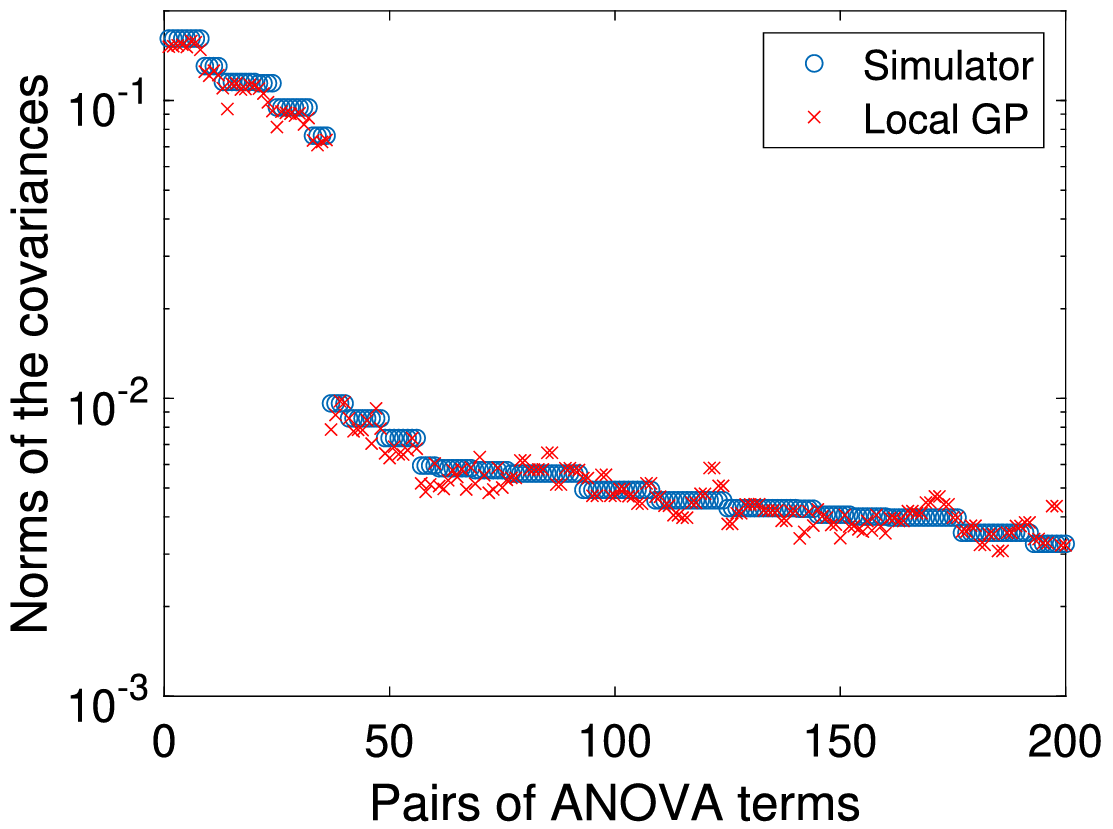 JCP
Journal of Computational Physics, Volume 416, 1 September 2020
JCP
Journal of Computational Physics, Volume 416, 1 September 2020
Services
Conference Reviewers
IEEE VIS: Visualization & Visual Analytics, 2023, 2024, 2025 The ACM CHI conference on Human Factors in Computing Systems, 2024 Eurographics, 2025 IEEE Pacific Visualization Symposium (PacificVis), 2024, 2025
Journal Reviewers
Powered by Jekyll and Minimal Light theme.